
Hệ trục tọa độ Descartes và ứng dụng trong công nghiệp
Hệ tọa độ Descartes được sử dụng rộng rãi trong lĩnh vực toán học, thiết kế đồ họa và một số ứng dụng để xác định vị trí của một điểm trên mặt phẳng hoặc trong không gian đa chiều. Điểm chung của hệ Descartes là một hoặc nhiều trục đi qua gốc tọa độ O. Từ đó, các điểm xuất hiện và chúng ta có thể xác định vị trí của chúng. Vậy, hệ trục tọa độ Descartes có những điểm gì đặc biệt? Cùng VTECH tìm hiểu trong bài viết sau đây nhé!
Hệ tọa độ Descartes là gì? Lịch sử hình thành
Hệ tọa độ Descartes (tên tiếng Anh: Cartesian coordinate system) là vị trí của một điểm trên mặt phẳng. Điểm này được xác định dựa trên cặp số tọa độ x và y. Trong đó, giá trị của x và y lần lượt nằm trên 2 đường thẳng vuông góc với nhau, chúng có chung một đơn vị đo.
René Descartes - Nhà toán học người Pháp, cha đẻ của hệ trục tọa độ Descartes. Mặc dù được phát triển từ thế kỷ 17, nhưng đây vẫn là hệ tọa độ có giá trị sử dụng đến thời điểm hiện tại. Hệ tọa độ này lần đầu tiên được giới thiệu thông qua bài phương pháp luận Pour bien conduire sa raison và phát triển sâu hơn trong bài La Géométrie.

Hệ tọa độ của ông đã tạo ra một liên kết giữa đại số và hình học Euclide. Ngoài ra, hệ tọa độ Descartes là nên tảng của hình học giải tích, giúp biểu diễn các đường thẳng, đường cong và các hình học trong mặt phẳng đa chiều. Ví dụ, một vòng tròn có tâm ở điểm có tọa độ (x,y) và bán kính bằng 2 (cm) được đưa ra bởi phương trình như sau: x2+y2=22.
Giải thích thuật ngữ hệ tọa độ Descartes
Để có thể hiểu được hệ trục tọa độ Descartes, chúng ta hãy cùng phân tích các thuật ngữ sau đây:
- Hai đường thẳng vuông góc với nhau được được đặt tên là trục X và trục Y. Khi 2 đường thẳng này được ghép lại với nhau được gọi là trục tọa độ của hệ.
- Trục X (trục hoành) là đường thẳng nằm ngang.
- Trục Y (trục tung) là đường thẳng thẳng đứng.
- Mặt phẳng được gọi là Descartes hay mặt phẳng tọa độ.
- Góc phần tư là tên gọi của 4 phần được chia bởi hai trục tọa độ.
- Góc tọa độ là điểm giao nhau giữa trục hoành và trục tung, ký hiệu là O, giá trị (0,0).
- Điểm P bất kỳ được xác định bằng một cặp giá trị x,y. Trong đó, giá trị tại x, y lần lượt được xác định thông qua đường thẳng song song với Oy và Ox. Bạn có thể tham khảo trong hình minh họa bên dưới.
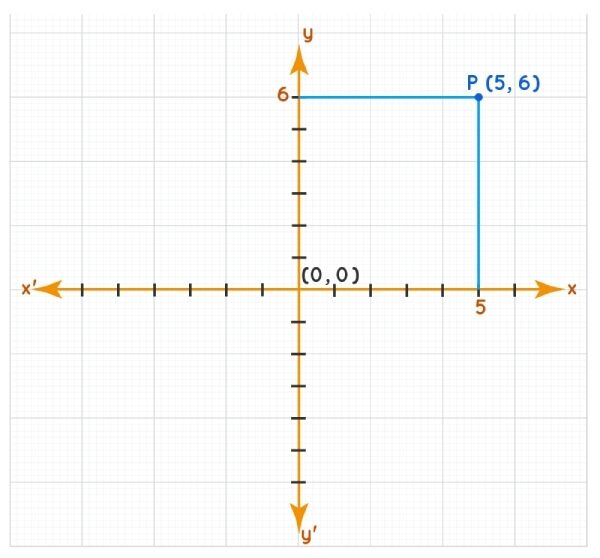
Các hệ trục tọa độ Descartes thường gặp
Hiện nay, có ba hệ tọa độ Descartes chính được sử dụng phổ biến trong nhiều lĩnh vực là hệ tọa độ một chiều, hai chiều và ba chiều.
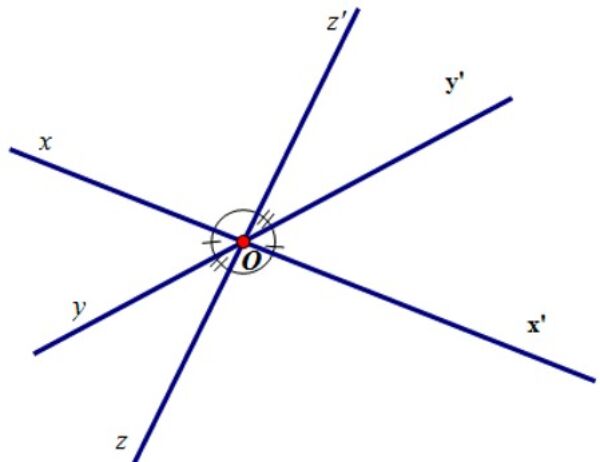
Hệ tọa độ Descartes một chiều
Hiểu đơn giản là hệ trục tọa độ chỉ có một trục hoành hoặc trục tung đi qua gốc tọa độ O. Đường thẳng này kéo dài từ phần âm đến phần dương. Nếu đường thẳng là trục hoành thì phần dương nằm bên phải gốc tọa độ và phần âm nằm bên trái. Tương tự, nếu đường thẳng là trục tung thì phần dương nằm ở trên gốc tọa độ và phần âm nằm bên dưới gốc tọa độ.
Mỗi điểm trên đường thẳng được xác định bằng cách tham chiếu đến điểm gốc với một tỷ lệ xác định. Tọa độ của điểm được bắt đầu bằng dấu “+” hoặc dấu “-” và giá trị số thực biểu thị khoảng cách của điểm đó đến gốc tọa độ. Hiểu đơn giản thì hệ tọa độ Descartes một chiều là đường số và bất kỳ số thực R nào cũng có thể biểu hiện trên đây.
Hệ tọa độ trên mặt phẳng (hai chiều - 2D)
Hệ tọa độ Descartes hai chiều hay còn được gọi là mặt phẳng tọa độ. Hai đường thẳng trục hoành và trục tung cắt mặt phẳng này thành bốn phần được gọi là góc phần tư. Ngoài ra, điểm giao giữa trục hoành và trục tung được gọi là góc tọa độ.
Giá trị của các điểm trên các góc phần tư được tham chiếu như sau:
- Góc phần tư thứ nhất (x,y).
- Góc phần tư thứ hai (-x,y).
- Góc phần tư thứ ba (-x,-y).
- Góc phần tư thứ tư (x,-y).
>> Xem thêm: Cách sử dụng máy đo 2D hiệu quả qua phần mềm FormFit
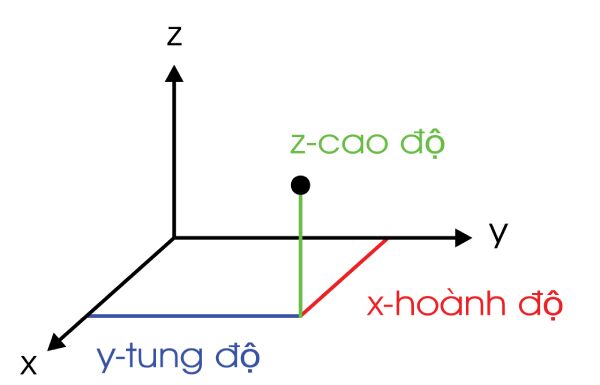
Hệ tọa độ trong không gian (ba chiều - 3D)
Khác với hệ tọa độ trên mặt phẳng, hệ tọa độ trong không gian được biểu thị bởi trục x, trục y và trục z. Những trục này vuông góc với nhau và biểu thị giá trị số theo cùng đơn vị đo. Tương tự như hệ trục 2 chiều, gốc tọa độ của hệ trục 3 chiều vẫn là điểm O, với giá trị (0,0,0). Ngoài ra, hệ tọa độ này chia không gian thành tám phần.
Bất kỳ điểm nào trong hệ tọa độ không gian cũng được cá định bởi tọa độ (x,y,z), với x, y, z được gọi lần lượt là hoành độ, tung độ và cao độ.
Hơn nữa, tọa độ của một điểm trong tám phần tám được biểu diễn dưới dạng (+ x, + y, + z), (-x, + y, + z), (+ x, + y, -z), (-x, + y, -z), (+ x, -y, + z), (-x, -y, + z), (+ x, -y, -z), (-x, -y, -z) .
Lưu ý: Hệ tọa độ Cartesian có thể có một hệ n chiều để biểu diễn nhiều đại lượng cùng một lúc. Nhưng các kích thước cao hơn không thể được trình bày dưới dạng hình học và chỉ giả định trên lý thuyết. Các hệ thống chiều cao hơn có các ứng dụng chính trong lập trình máy tính và trí tuệ nhân tạo.
Những lưu ý quan trọng về hệ tọa độ Descartes
Một số lưu ý khi sử dụng hệ tọa độ Descartes như sau:
- Giao điểm của cả hai trục được gọi là điểm gốc và tọa độ của nó là (0, 0).
- Có thể có vô số điểm trên một mặt phẳng tọa độ Descartes.
- Các điểm nằm trên bất kỳ trục số nào không thuộc bất kỳ góc phần tư nào.
- Một điểm nằm trên trục x có tọa độ y là dương và nếu điểm nằm dưới trục x thì tọa độ y của nó là âm.
- Một điểm nằm bên phải trục y có tọa độ x dương và nếu điểm nằm bên trái trục y thì tọa độ x âm.
Qua bài viết, chúng ta có thể thấy được hệ tọa độ Descartes rất quan trọng trong niều lĩnh vực như: xây dựng, chế tạo,… Đây là nền tảng cơ bản, tạo tiền đề để phát triển các lĩnh vực khác, đặc biệt là công nghệ 4.0. Hệ thống máy đo quang học của VTECH có thể phác thảo chi tiết kết cấu đa chiều dựa trên hoạt động của hệ tọa độ này. Để biết thêm chi tiết vui lòng liên hệ với chúng tôi thông qua hotline.
Link nội dung: https://pus.edu.vn/he-truc-toa-do-a64096.html