Chuyển động tròn đều là gì? Các đại lượng đặc trưng và công thức tính cần nhớ

Chuyển động tròn đều là gì

Trong đời sống hằng ngày, chúng ta thường nhìn thấy những hình ảnh quen thuộc như kim đồng hồ xoay, vòng đu quay trong công viên giải trí,... những hình ảnh này đều được gọi là chuyển động tròn. Vậy chuyển động tròn đều khác với chuyển động tròn như thế nào?

• Khi chuyển động có quỹ đạo là một đường tròn, ta gọi nó là chuyển động tròn.

• Tốc độ trung bình trong chuyển động tròn sẽ bằng thương của độ dài cung tròn mà vật đi được so với thời gian chuyển động của vật.

Tốc độ trung bình trong chuyển động tròn = (độ dài cung tròn mà vật đi được) / (thời gian chuyển động)

Chuyển động tròn đều là chuyển động có quỹ đạo tròn và trong những khoảng thời gian bằng nhau bất kì, vật đi được những cung tròn bằng nhau.

Tốc độ dài, tốc độ góc, chu kỳ, tần số trong chuyển động tròn đều

Tốc độ dài trong chuyển động tròn đều

Gọi Δs là độ dài cung tròn mà vật đi được trong khoảng thời gian rất ngắn, ta có công thức tính tốc độ dài (độ lớn tức thời trong chuyển động tròn đều) như sau:

v = Δs/Δt

Trong chuyển động tròn đều, tốc độ dài của vật sẽ không thay đổi.

Vectơ vận tốc trong chuyển động tròn đều

Xét trên điều kiện cung tròn có độ dài rất nhỏ (có thể như một đường thẳng), ta dùng một vectơ để chỉ quãng đường vừa đi được, vừa để chỉ hướng chuyển động.

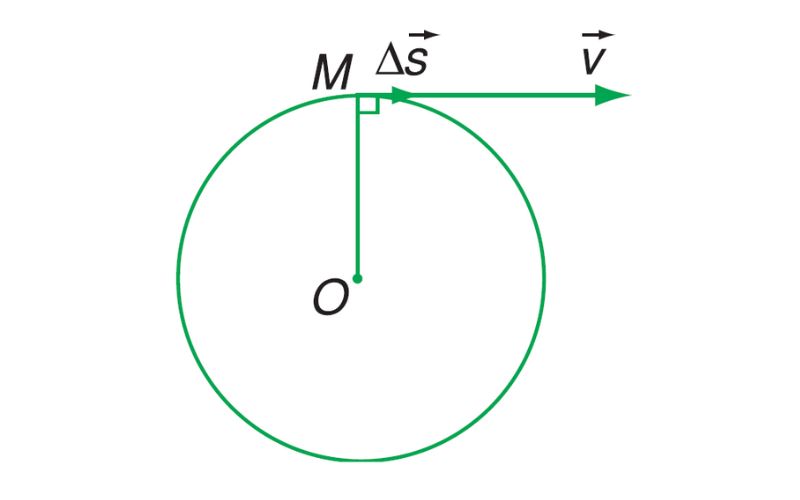
Vectơ vận tốc trong chuyển động tròn đều luôn có phương tiếp tuyến với đường tròn quỹ đạo.

Trong chuyển động tròn đều, phương của vectơ vận tốc luôn luôn thay đổi.

Tốc độ góc trong chuyển động tròn đều

Tốc độ của chuyển động tròn đều chính là đại lượng được đo bằng góc mà bán kính OM (hình ảnh dưới) quét được trong một đơn vị thời gian. Tốc độ góc của chuyển động tròn đều là đại lượng không đổi.

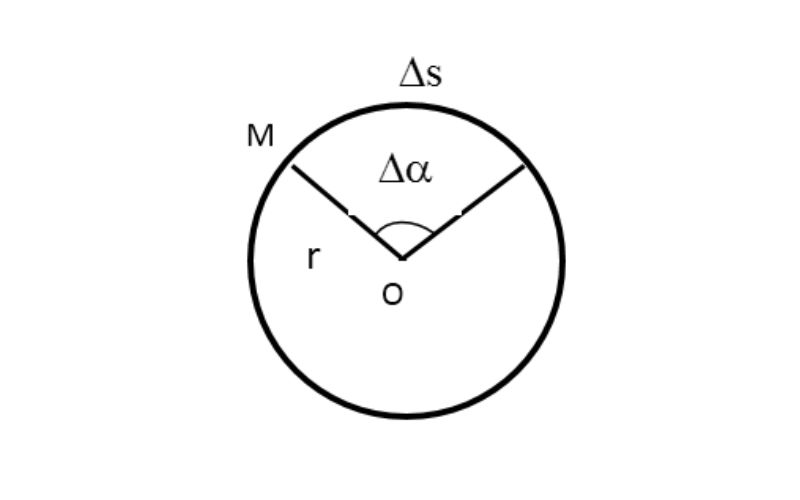
Ta có công thức tốc độ góc:

ω = Δα/Δt

Trong đó:

• ω : tốc độ góc, đơn vị đo rad/s

• Δα : bán kính góc OM quét được, đơn vị đo radian (rad)

• Δt : thời gian bán kính OM quét, đơn vị đo giây (s)

Công thức liên hệ giữa tốc độ dài và tốc độ góc

Công thức:

v = r . ω

Trong đó

• v : tốc độ dài (m/s)

• r : bán kính (m)

• ω : tốc độ góc (rad/s)

Chu kỳ trong chuyển động tròn đều

Chu kì T của chuyển động tròn đều là thời gian để vật đi được một vòng. Đơn vị đo của chu kì là giây (s).

Ta có công thức:

T = 2π/ω

Tần số trong chuyển động tròn đều

Tần số f của chuyển động tròn đều là số vòng mà vật đi được trong một giây. Đơn vị của tần số là vòng/s hoặc hec (Hz).

Ta có công thức:

f = 1/T

Gia tốc hướng tâm

Vectơ gia tốc trong chuyển động tròn đều có hướng như thế nào?

Trong chuyển động tròn đều, hướng luôn thay đổi dù vận tốc có độ lớn không đổi, nên chuyển động này có gia tốc. Gia tốc trong chuyển động tròn đều luôn hướng vào tâm của quỹ đạo nên được gọi là gia tốc hướng tâm.

Độ lớn của gia tốc hướng tâm

Công thức tính độ lớn của gia tốc hướng tâm:

Trong đó:

• a(ht) : gia tốc hướng tâm (m/s^2)

• v : tốc độ dài (m/s)

• r : bán kính (m)

• ω : tốc độ góc (rad/s)

Xem thêm: Chuyển động cơ là gì? Chất điểm là gì? Lý thuyết & bài tập chi tiết (Vật lý 10)

Bài tập chuyển động tròn đều Vật Lý 10

Bài 1: Chuyển động của vật nào dưới đây được coi là chuyển động tròn đều?

A. Chuyển động quay của bánh xe ô tô khi đang hãm phanh.

B. Chuyển động quay của kim phút trên mặt đồng hồ chạy đúng giờ.

C. Chuyển động quay của của điểm treo các ghế ngồi trên chiếc đu quay.

D. Chuyển động quay của cánh quạt khi vừa tắt điện.

Bài 2: Chuyển động tròn đều có

A. vectơ vận tốc không đổi.

B. tốc độ dài phụ thuộc vào bán kính quỹ đạo.

C. tốc độ góc phụ thuộc vào bánh kính quỹ đạo.

D. gia tốc có độ lớn phụ thuộc vào bán kính quỹ đạo.

Bài 3: Phát biểu nào sau đây là chính xác? Trong chuyển động tròn đều:

A. vectơ vận tốc luôn không đổi, do đó gia tốc bằng 0.

B. gia tốc hướng vào tâm quỹ đạo, độ lớn tỉ lệ nghịch với bình phương tốc độ dài.

C. phương, chiều và độ lớn của vận tốc luôn thay đổi.

D. gia tốc hướng vào tâm quỹ đạo, độ lớn tỷ lệ với bình phương tốc độ góc

Bài 4: Chọn câu đúng.

A. Trong các chuyển động tròn đều có cùng bán kính, chuyển động nào có chu kỳ quay lớn hơn thì có vận tốc dài lớn hơn.

B. Trong chuyển động tròn đều, chuyển động nào có chu kỳ quay nhỏ hơn thì có vận tốc góc nhỏ hơn.

C. Trong các chuyển động tròn đều, chuyển động nào có tần số lớn hơn thì có chu kỳ nhỏ hơn.

D. Trong các chuyển động tròn đều, với cùng chu kỳ, chuyển động nào có bán kính nhỏ hơn thì có vận tốc góc nhỏ hơn.

Bài 5: Các công thức liên hệ giữa tốc độ góc ω với chu kỳ T và giữa tốc độ góc ω với tần số f trong chuyển động tròn đều là:

A. ω = 2π/T; ω = 2πf

B. ω = 2πT; ω = 2π/f.

C. ω = 2πT; ω = 2π/f

D. ω = 2π/T; ω = 2π/f

Bài 6: Một điểm nằm ngoài cùng cánh quạt có chiều dài 30cm chuyển động tròn đều với chu kỳ quay là 0,2s. Xác định tốc độ dài và tốc độ góc của điểm đó.

Bài 7: Một chất điểm chuyển động tròn đều trong một phút quay được 300 vòng. Xác định tốc độ dài, tốc độ góc và độ lớn gia tốc hướng tâm của chất điểm biết bán kính quỹ đạo tròn là 40cm

Bài 8: Xác định tỉ số giữa tốc độ góc, tỉ số giữa tốc độ dài, tỉ số giữa gia tốc hướng tâm của chất điểm nằm trên đầu kim phút dài 4cm, kim giờ dài 3cm,

Bài 9: Xác định chu kỳ quay, tốc độ góc, gia tốc hướng tâm của một chất điểm chuyển động tròn đều với tốc độ 64,8 km/h trên quỹ đạo có bán kính 30cm.

Bài 10: Coi chuyển động của Trái Đất quanh Mặt Trời là chuyển động tròn đều và chuyển động tự quay quanh mình của Trái Đất cũng là chuyển động tròn đều. Biết bán kính của Trái Đất là 6400km, Trái Đất cách Mặt Trời 150 triệu km, Chu kỳ quay của Trái Đất quanh Mặt Trời là 365 ngày và 1/4 ngày Trái Đất tự quay quanh mình nó mất 1 ngày. Tính

a) Tốc độ góc và tốc độ dài của tâm Trái Đất trong chuyển động tròn quanh Mặt Trời

b) Tốc độ góc và tốc độ dài của một điểm nằm trên đường xích đạo trong chuyển động tự quay quanh mình của Trái Đất.

c) Tốc độ góc và tốc độ dài của một điểm nằm trên vĩ tuyến 30 trong chuyển động tự quay quanh mình của Trái Đất

Hướng dẫn giải:

Bài 1: B

Bài 2: D

Bài 3: D

Bài 4: C

Bài 5: A

Bài 6: Phân tích bài toán

r = 30cm = 0,3m; T = 0,2s

Giải

ω = 2π/T = 10π rad/s.

v = rω = 9,42 m/s.

Bài 7: Phân tích bài toán

ω = 300vòng/phút = 300.2π/60 (rad/s) = 10π (rad/s); r = 40cm = 0,4m

Giải

ω = 10π (rad/s)

v = rω = 0,4.10π = 12,56 m/s.

a(ht)=v^2/r = 394,4 m/s2.

Bài 8: Phân tích bài toán

Kim phút: T1 = 3600s; r1 = 4 cm = > ω1 = 2π/T1; v1 = ω1.r1; a1 = ω12.r1

Kim giờ: T2 = 12*3600s; r2 = 3cm = > ω2 = 2π/T2; v2 = ω2.r2; a2 = ω22.r2

Giải

ω1/ ω2 = 12

v1/v2 = 16

a1/a2 = 192

Bài 9: Phân tích bài toán

v = 64,8km/h = 18m/s; r = 30cm

Giải

ω = v/r = 60 rad/s.

T = 2π/ ω = 0,1s

aht= ω2r = 1080 m/s2.

Bài 10: Phân tích bài toán

a/ r = 150 triệu km = 150.109m; T1 = 365,25 ngày = 365,25*24*3600 (s)

b/ R = 6400km = 6400.103m; T2 = 24h = 24*3600 (s)

c/ R = 6400km.cos30o ; T3 = 24h = 24*3600 (s)

Giải

a/ ω1 = 2π/T1 = 2.10-7 (rad/s);

v1 = ω1(r + R) = 30001 m/s.

b/ ω2 = 2π/T2 = 7,27.10-5 (rad/s);

v2 = ω2R = 465 m/s.

c/ ω3 = 2π/T3 = 7,27.10-5(rad/s);

v3 = ω3Rcos30o = 402 m/s.

Chuyển động tròn đều xuất hiện xung quanh chúng ta hàng ngày, hàng giờ, thế nhưng không phải ai cũng biết được bản chất cũng như cách tính những đại lượng của nó. Hy vọng rằng, qua bài viết này các em có thể hiểu và áp dụng để giải quyết các bài toán liên quan trong chương trình vật lý 10 này nhé!