1. Định nghĩa:
Giả sử phương trình (1) xác định với u, v là hàm số của các biến độc lập x và y: (2) thì khi đó z được gọi là hàm số hợp của các biến số x và y thông qua 2 biến trung gian u và v.
Như vậy z cũng có thể biểu diễn như hàm 2 biến x, y: 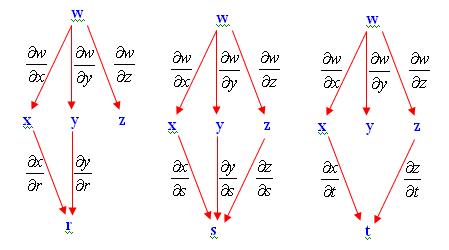 (3)
(3)
Ví dụ: Cho
Khi đó:
Tình huống:
Nếu ta cần khảo sát đạo hàm của hàm số hợp thì có thể viết hàm số dưới dạng tường minh theo 2 biến x, y. Tuy nhiên, với hàm trên thì việc lấy đạo hàm riêng sẽ rất khó khăn. Hoặc nếu hàm số chưa xác định được công thức, ví dụ: hoặc thì làm sao tính được các đạo hàm riêng
2. Định lý: (Tính từ (1), (2) mà không dùng (3)
Cho z = f(u,v) và u, v là các hàm của hai biến u = u(x,y) và v = v(x,y). Cho các hàm z, u, v khả vi tại các điểm tương ứng. Khi đó, z = f(u,v) có các đạo hàm riêng xác định bởi công thức:
;
3. Quy tắc Xích để xác định công thức tính đạo hàm cho hàm hợp:
- Dòng 1: Viết hàm cần tính đạo hàm z
- Dòng 2: Xác định các biến trung gian có trong hàm z. Ví dụ: (u,v)
- Dòng 3: xác định biến cần lấy đạo hàm. Ví dụ x
- Nối z với các biến trung gian u, v bằng những đoạn kẻ. Mỗi đoạn kẻ tương ứng với phép lấy đạo hàm.
- Nếu u, v là những biến phụ thuộc x thì nối u với x bằng 1 đường kẻ; nối v với x bằng 1 đường kẻ. Các đường kẻ trên chính là các phép toán lấy đạo hàm riêng.
- Tổng hợp tất cả các cách nối được từ z đến x ta sẽ có công thức tính đạo hàm của z theo x.
4. Một số trường hợp tổng quát:
1. Với z = f(u,v, w) , trong đó u = u(t), v = v(t), w = w(t)
Khi đó: z là hàm số hợp của 1 biến số t thông qua 3 biến trug gian u, v, w.
Bấy giờ, đạo hàm của z theo t được xác định
(do z, u, v, w đều là hàm theo 1 biến t nên đạo hàm là đạo hàm thường)
Áp dụng: tính , nếu , với
Tương tự quy tắc trên, ta có:
Nghĩa là:
Hay:
Ví dụ 1: Tính nếu với y = f(x).
Trong ví dụ này, ta cần chú ý và phân biệt ý nghĩa của hai ký hiệu
Đầu tiên, ký hiệu chỉ z là hàm theo 1 biến x, trong khi đó, biểu thức xác định của z là: nên với ký hiệu này ta sẽ hiểu là z là hàm số hợp của 1 biến x thông qua biến trung gian y.
Còn ký hiệu, chỉ đạo hàm riêng của z theo biến x, điều này được hiểu là z là hàm hai theo 2 biến độc lập x, y.
Như vậy:
Còn:
Ví dụ 2: Tìm biết
Bạn có thể lập sơ đồ xích cho 3 biến r, s, t để xác định công thức tính đạo hàm như sau:
Dựa vào sơ đồ trên, ta có:
,
Việc còn lại bạn làm tiếp tục nhé.
Ví dụ 3: Tìm
Ta đặt: thì f là hàm số hợp của 2 biến x, y thông qua 2 biến trung gian u, v.
Khi đó:
4. Đạo hàm cấp 2 của hàm số hợp 2 biến:
Giả sử z là hàm số hợp theo 2 biến x, y thông qua 2 biến trung gian u, v. Khi đó ta đã có công thức tính đạo hàm riêng cấp 1 của z đối với 2 biến x, y. Vấn đề đặt ra là: vậy nếu cần tính tiếp tục đạo hàm riêng cấp 2 của hàm số hợp thì ta phải làm thế nào?
Ta chú ý, trong công thức:
Các đại lượng lại là các biểu thức theo u, v nên nó lại là những hàm số hợp của hai biến x, y thông qua 2 biến trung gian u, v.
Do đó:
(*)
Mặt khác, áp dụng quy tắc tính đạo hàm hàm số hợp cho 2 hàm . Ta có:
, (**)
Từ (*), (**) ta có:
Hoàn toàn tương tự, ta tìm được công thức xác định (bạn thử tìm xem nhé)
Ví dụ áp dụng: Tìm nếu
Đáp số:
Tình huống:
Cho y là hàm theo biến số x xác định từ phương trình: .Bạn thử tìm đạo hàm: .
Nếu giải tìm được y theo x thì bài toán quá dễ dàng. Còn nếu không giải tìm được hàm y theo biến x thì thế nào đây?


